When integrating our plug-and-play training strategies ([D,R]) into the state-of-the-art
learning-based models such as
RIFE [1],
IFRNet [2],
AMT [3], and
EMA-VFI [4], they exhibit markedly
sharper outputs and superior perceptual quality in arbitrary time interpolations.
(Here, we employ RIFE as an illustrative example, generating 128 interpolated frames
using just two images.)
Our technology was used by CCTV5 as well as CCTV5+ for slow motion demonstrations of athletes jumping in the 2024 Thomas & Uber Cup.
Additionally, our strategies enable temporal manipulation of each object independently during the inference stage, offering a novel tool for video editing tasks like re-timing. Our APP also supports video as an input to classic video frame interpolation.
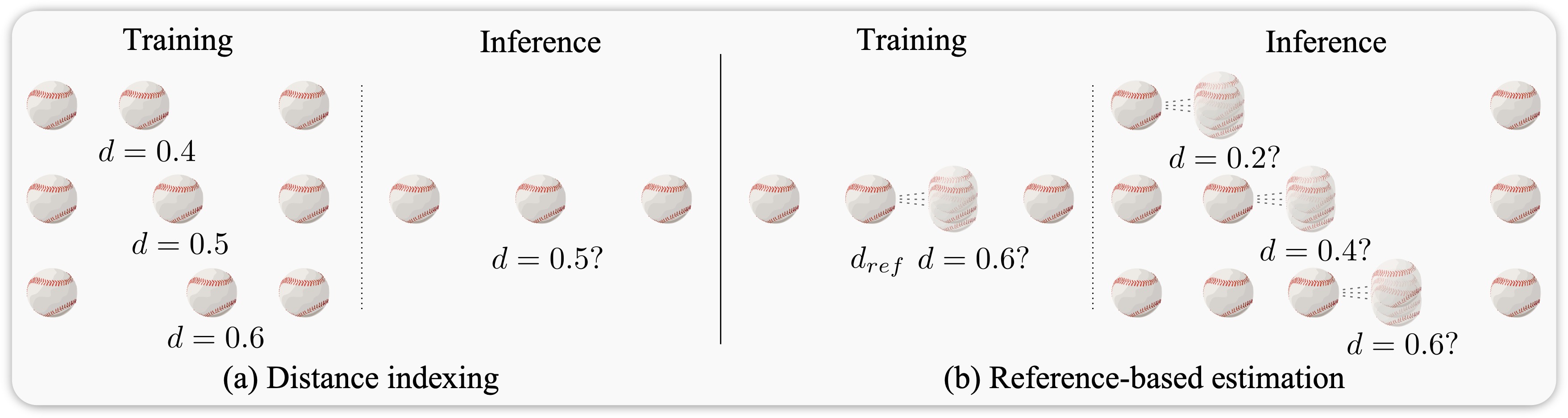
Existing video frame interpolation (VFI) methods blindly predict where each object is at a specific timestep t ("time indexing"), which struggles to predict precise object movements. Given two images of a ⚾, there are infinitely many possible trajectories: accelerating or decelerating, straight or curved. This often results in blurry frames as the method averages out these possibilities. Instead of forcing the network to learn this complicated time-to-location mapping implicitly together with predicting the frames, we provide the network with an explicit hint on how far the object has traveled between start and end frames, a novel approach termed "distance indexing". This method offers a clearer learning goal for models, reducing the uncertainty tied to object speeds. We further observed that, even with this extra guidance, objects can still be blurry especially when they are equally far from both input frames (i.e., halfway in-between), due to the directional ambiguity in long-range motion. To solve this, we propose an iterative reference-based estimation strategy that breaks down a long-range prediction into several short-range steps. When integrating our plug-and-play strategies into state-of-the-art learning-based models, they exhibit markedly sharper outputs and superior perceptual quality in arbitrary time interpolations, using a uniform distance indexing map in the same format as time indexing. Additionally, distance indexing can be specified pixel-wise, which enables temporal manipulation of each object independently, offering a novel tool for video editing tasks like re-timing.
The current mainstream algorithm for arbitrary-time frame interpolation, denoted as \(\mathcal{F}\), predicts the target frame \(I_t\) using the starting frame \(I_0\), the ending frame \(I_1\), and a time index \(t\) as inputs: $$I_t = \mathcal{F}\left(I_0, I_1, t\right)$$ However, the unknown motion velocity of each independently moving object introduces the issue of "velocity ambiguity". This means there are multiple possible mappings from the same inputs to different locations: $$\left\{I_t^1, I_t^2, \ldots, I_t^n\right\} = \mathcal{F}(I_0, I_1, t)$$ Taking a ⚾ as an example, there are countless potential landing spots for the ball in mid-air, leading to conflicts in learning during the training process. In short, the algorithm cannot discern which scenario is correct to learn, so it settles for an average state: $$ \hat{I}_t = \mathbb{E}_{I_t \sim \mathcal{F}(I_0, I_1, t)}[I_t] $$ This results in the algorithm's prediction \(\hat{I}_t\) being blurry during testing:

To resolve velocity ambiguity, a new paradigm for index-based learning is required. We need to guide the algorithm on why objects land in certain positions: $$I_{t} = \mathcal{F}\left(I_0, I_1, \text{motion hint}\right)$$
In fact, the training approach using time indexing requires the algorithm to not only learn how to interpolate frames but also to guess the mapping relationship from time to position, denoted as \(\mathcal{D}\): $$I_t = \mathcal{F}(I_0, I_1, t) \to I_t = \mathcal{F}(I_0, I_1, \mathcal{D}(t))$$ Our solution involves calculating a path distance ratio map \(D_t\) to replace the time \(t\) for index-based learning: $$I_t = \mathcal{F}(I_0, I_1, \mathcal{D}(t)) \to I_t = \mathcal{F}(I_0, I_1, D_t)$$

We first compute the optical flows from \(I_0\) to \(I_t\) and from \(I_0\) to \(I_1\), denoted as \(V_{0\to t}\) and \(V_{0\to 1}\), respectively. Then, for each pixel location \((x,y)\), we calculate the proportion of the optical flow \(V_{0\to t}\) projected onto \(V_{0\to 1}\), denoted as the "path distance ratio": $$D_t(x,y) = \frac{\left\Vert \mathbf{V}_{0\to t}(x,y)\right\Vert \cos{\theta}}{\left\Vert \mathbf{V}_{0\to 1}(x,y) \right\Vert}$$ With \(D_t\), the algorithm avoids the ambiguous time-to-position mappings during training caused by varying velocities, allowing for clearer predictions during testing. Importantly, even without the ability to calculate the exact \(D_t\) using ground truth labels during inference, providing a uniform index map similar to time indexing, i.e., \(D_t=t\), the algorithm can still predict clearer images (simulating uniform motion of objects).
While path distance indexing helps us sidestep ambiguities in speed, it does not resolve directional
ambiguities. We apply a classic divide-and-conquer strategy to minimize the impact of directional
ambiguities, further improving the predicted outcome.
In practice, we break down a long-distance inference into a series of short-distance inferences from
near to far, using the previous inference, along with the starting and ending frames, as references
to avoid accumulated errors:
$$I_t = \mathcal{F}(I_0, I_1, D_t, I_{\text{ref}}, D_{\text{ref}})$$
For example, dividing the inference into two steps would look like:
$$I_{t/2} = \mathcal{F}(I_0, I_1, D_{t/2}, I_{0}, D_{0})$$
$$I_{t} = \mathcal{F}(I_0, I_1, D_{t}, I_{t/2}, D_{t/2})$$
Similarly, taking a ⚾ as an example, our proposed strategies are illustrated in the following
figure:
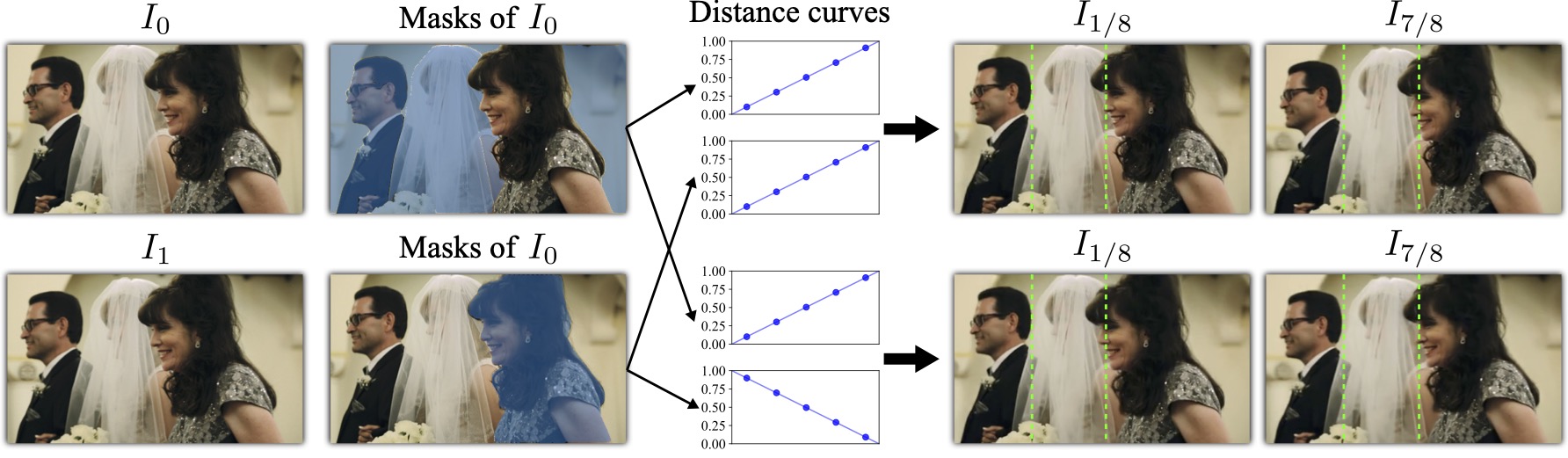
Beyond using a uniform index map like time indexing, we can also take advantage of the 2D editable nature of path distance indexing to implement editable frame interpolation techniques. Initially, we can obtain masks for objects of interest using the Segment Anything Model (SAM) [5]. We then customize the path distance curves for different object regions to achieve manipulated interpolation of anything.
This work presents the next generation of video frame interpolation technology, aiming to inspire
readers and contribute to fields like video enhancement, editing, and generation! 🔥🔥🔥
Welcome to 🌟 this project
and follow the author's GitHub~
@article{zhong2023clearer,
title={Clearer Frames, Anytime: Resolving Velocity Ambiguity in Video Frame Interpolation},
author={Zhong, Zhihang and Krishnan, Gurunandan and Sun, Xiao and Qiao, Yu and Ma, Sizhuo and Wang, Jian},
journal={arXiv preprint arXiv:2311.08007},
year={2023}}We thank Dorian Chan, Zhirong Wu, and Stephen Lin for their insightful feedback and advice. Our thanks also go to Vu An Tran for developing the web application, and to Wei Wang for coordinating the user study.
[1] Huang, Zhewei, Tianyuan Zhang, Wen Heng, Boxin Shi, and Shuchang Zhou. "Real-time intermediate flow
estimation for video frame interpolation." In European Conference on Computer Vision, pp. 624-642. Cham:
Springer Nature Switzerland, 2022.
[2] Kong, Lingtong, Boyuan Jiang, Donghao Luo, Wenqing Chu, Xiaoming Huang, Ying Tai, Chengjie Wang, and Jie
Yang. "Ifrnet: Intermediate feature refine network for efficient frame interpolation." In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 1969-1978. 2022.
[3] Li, Zhen, Zuo-Liang Zhu, Ling-Hao Han, Qibin Hou, Chun-Le Guo, and Ming-Ming Cheng. "AMT: All-Pairs
Multi-Field Transforms for Efficient Frame Interpolation." In Proceedings of the IEEE/CVF Conference on
Computer Vision and Pattern Recognition, pp. 9801-9810. 2023.
[4] Zhang, Guozhen, Yuhan Zhu, Haonan Wang, Youxin Chen, Gangshan Wu, and Limin Wang. "Extracting motion and
appearance via inter-frame attention for efficient video frame interpolation." In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5682-5692. 2023.
[5] Kirillov, Alexander, Eric Mintun, Nikhila Ravi, Hanzi Mao, Chloe Rolland, Laura Gustafson, Tete Xiao,
Spencer Whitehead, Alexander C. Berg, Wan-Yen Lo, Piotr Dollár, and Ross Girshick. "Segment Anything." In
Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 4015-4026. 2023